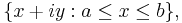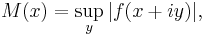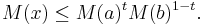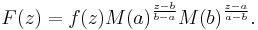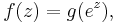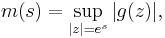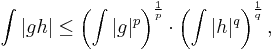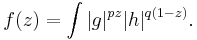Hadamard three-lines theorem

In complex analysis, a branch of mathematics, the Hadamard three-lines theorem, named after the French mathematician Jacques Hadamard, is a result about the behaviour of holomorphic functions defined in regions bounded by parallel lines in the complex plane.

Contents

Statement

Let f(z) be a bounded function of z = x + iy defined on the strip

\{x%2Biy:a\le x \le b\},

holomorphic in the interior of the strip and continuous on the whole strip. Then, if

M(x)=\sup_y |f(x%2Biy)|, \,

log M(x) is a convex function on [a, b].

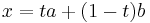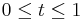In other words, if x=t a %2B (1-t) b with 0\le t \le 1, then

M(x)\le M(a)^t M(b)^{1-t}. \,

Proof

Define 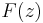F(z) by

F(z)=f(z) M(a)^{{z-b\over b-a}}M(b)^{{z-a\over a-b}}.

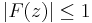Thus |F(z)|\le 1 on the edges of the strip.

The maximum modulus principle can be applied to 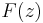F(z) in the strip in the form due to Phragmén and Lindelöf.

It shows that the same inequality holds throughout the strip.

This inequality is equivalent to the three lines theorem.

Applications

The three-line theorem can be used to prove the Hadamard three-circle theorem for a bounded continuous function 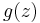g(z) on an annulus 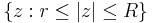\{z: r \le |z| \le R\}, holomorphic in the interior. Indeed applying the theorem to

f(z) = g(e^{z}), \,

shows that, if

m(s)=\sup_{|z|=e^s} |g(z)|, \,

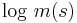then \log\, m(s) is a convex function of s.

The three-line theorem also holds for functions with values in a Banach space and plays an important rôle in complex interpolation theory, It can be used to prove Hölder's inequality for measurable functions

\int |gh|\le \left(\int |g|^p\right)^{1\over p} \cdot \left(\int |h|^q\right)^{1\over q},

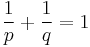where {1\over p} %2B {1\over q} =1, by considering the function

f(z) = \int |g|^{pz} |h|^{q(1-z)}.

See also

References